受限玻尔兹曼机
http://xiaosheng.me/2017/08/02/article83/ https://github.com/Syndrome777/DeepLearningTutorial/blob/master/7_Restricted_Boltzmann_Machine_%E5%8F%97%E9%99%90%E6%B3%A2%E5%B0%94%E5%85%B9%E6%9B%BC%E6%9C%BA.md
1. 能量模型
基于能量模型(Energy-Based Models)
- 2006 年,杰弗里·辛顿提出了一种深度信念网络(Deep Belief Network),并提出学习算法
可以直接自动地从训练集里提取所需要的特征,典型的模型为受限玻尔兹曼机(RBM)
能量模型来源于热动力学。分子在高温中运动剧烈,能够克服局部约束,在逐步降到低温时,分子最终会排列出有规律的结构,此时也是低能量状态,即最终的稳态对应于某一种能量的最低状态。
* 能量模型和波兹曼机的关系
统计力学的结论表明,任何概率分布都可以转变成基于能量的模型,而且很多的分布都可以利用能量模型的特有性质和学习过程,有些甚至从能量模型中找到了通用的学习方法。
能量模型需要做的事情就是定义一个合适的能量函数,然后基于这个能量函数得到变量的概率分布,最后基于概率分布求解一个目标函数(如最大似然)。
* 玻尔兹曼机(Boltzmann machine, BM)是源于物理学的能量函数的建模方法
- 玻尔兹曼网络是一种随机网络
* 随机网络的建模方法
概率分布函数:由于网络节点的取值状态是随机的,从贝叶斯网的观点来看,要描述整个网络,需要用三种概率分布来描述系统,即联合概率分布、边缘概率分布和条件概率分布。
能量函数:随机神经网络是根植于统计力学的。我们就是要找到系统最稳定的状态,也就是要找到能量函数最小值。
受统计力学中能量泛函的启发,引入了能量函数。能量函数是描述整个系统状态的一种测度。系统越有序或者概率分布越集中,系统的能量越小。反之,系统越无序或者概率分布越趋于均匀分布,则系统的能量越大。能量函数的最小值,对应于系统的最稳定状态
2. 受限玻尔兹曼机(RBM)
2.1 结构
- 受限玻尔兹曼机包括隐层、可见层和偏置层。
- RBM在可见层和隐层间的链接是方向不定的(值可以进行双向传播)和完全链接的。
- 在标准 RBM 中,隐含和可见层的神经元都是二进制表示(即神经元的激活值只能是服从伯努利分布的 0 或 1),不过也存在其他非线性的变种。
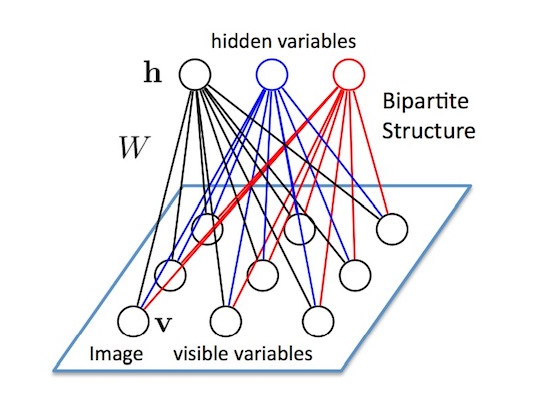
- 假设有一个二部图如上图所示,每一层的节点之间没有链接,一层是可视层,即输入数据层 V,一层是隐藏层 h,如果所有节点都是随机二进制变量节点(只能取 0 或者 1),同时假设全概率分布 p(v,h)满足 Boltzmann 分布,称这个模型是 RBM。
* 上述图,n个可视节点和m个隐藏节点,每个可视节点只和m个隐藏节点相关
* RBM的参数
- 可视层与隐藏层之间的权重矩阵$$W_{m*n}$$
- 一个是可视节点的偏移量 :$$b=(b_1,b_2,..,b_n)$$
- 一个是隐藏节点的偏移量: $$c=(c_1,c_2,...,c_m)$$
* RBM 网络将一个 n 维的样本编码成一个什么样的 m 维样本。

3. RBM的用途
对数据编码,然后交给监督学习方法进行分类或者回归(降维方法) * 得到权重矩阵和偏移量,供BP 神经网络初始化训练。
神经网络要训练一个权重矩阵和偏移量,如果直接使用 BP 神经网络,初始值选得不好的话,往往会陷入局部极小值。实验结果表明,直接把 RBM 训练得到的权重矩阵和偏移量作为 BP 神经网络的初始值,得到的结果会非常好。
4. 能量模型的公式
- 基于能量的模型(EBM)把我们所关心变量的各种组合和一个标量能量联系在一起。训练模型的过程就是不断改变标量能量的过程,使其能量函数的形状满足期望的形状。比如,如果一个变量组合被认为是合理的,它同时也具有较小的能量。
$$p(x)=\frac{e^{-E(x)}}{Z}$$
其中:Z是归一化因子:$$Z=\sum\limits_{x} e^{-E(x)}$$
* 满足能量函数的任意分布是玻尔兹曼分布
- 能量模型可以通过SGD来学习,类似逻辑回归
5. 受限玻尔兹曼机
- 对数线性马尔可夫随机场(MRF)的一种特殊形式,
- 一些变量是不可见的(被称为隐藏)